Sums of squares – characterization and distribution
- Greg Martin | University of British Columbia
We survey some of the important and classical facts concerning integers that can be written as the sum of (two, three, or four) squares, as well as the number of such representations, emphasizing the connection to multiplicative functions. We include sketches of proofs of the characterizations of such integers and of Landau’s theorem on the number of integers that can be represented as the sum of two squares. Finally, we discuss the distribution of such integers in short intervals (including a brief description of sieve methods) and speculate on related questions involving lattice points in thin regions of the plane.
-
-
Jeff Running
-
-
Series: Microsoft Research Talks
-
Decoding the Human Brain – A Neurosurgeon’s Experience
- Dr. Pascal O. Zinn
-
-
-
-
-
-
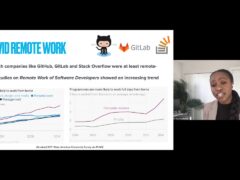
Challenges in Evolving a Successful Database Product (SQL Server) to a Cloud Service (SQL Azure)
- Hanuma Kodavalla,
- Phil Bernstein
-
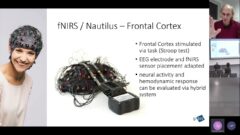
Improving text prediction accuracy using neurophysiology
- Sophia Mehdizadeh
-
Tongue-Gesture Recognition in Head-Mounted Displays
- Tan Gemicioglu
-
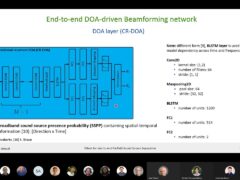
DIABLo: a Deep Individual-Agnostic Binaural Localizer
- Shoken Kaneko
-
-
-
-
Audio-based Toxic Language Detection
- Midia Yousefi
-
-
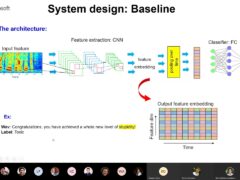
From SqueezeNet to SqueezeBERT: Developing Efficient Deep Neural Networks
- Forrest Iandola,
- Sujeeth Bharadwaj
-
Hope Speech and Help Speech: Surfacing Positivity Amidst Hate
- Ashique Khudabukhsh
-
-
-
Towards Mainstream Brain-Computer Interfaces (BCIs)
- Brendan Allison
-
-
-
-
Learning Structured Models for Safe Robot Control
- Subramanian Ramamoorthy
-