Scientific research is a continuous journey fueled by curiosity and collaboration, a conversation between scientists that often crosses continents and spans decades, with each new discovery inspired by and expanding on the work of others. The story of density functional theory (DFT), the fundamental method in chemistry and physics for predicting the formation and properties of molecules and materials, began nearly a century ago.
The timeline below highlights some key milestones in the DFT journey, including the recent introduction of the Skala XC Functional, the new deep-learning-powered DFT model developed by Microsoft Research. But the DFT journey is far from over. It will continue, step by step, with new advancements and new breakthroughs in fields ranging from drug discovery to materials science.
To learn more about the work Microsoft Research is doing on DFT, explore Breaking bonds, breaking ground: Advancing the accuracy of computational chemistry with deep learning. Or visit Microsoft Research to learn more about other scientific research currently underway at Microsoft.
-
1926
Schrödinger equation
Physicist Erwin Schrödinger develops the equation that bears his name, which is to quantum mechanics what Newton’s laws of motion are to classical mechanics. The Schrödinger equation is a differential equation that describes how matter behaves at the atomistic scale, when classical mechanics ceases to be accurate. It tells us how the wave function—used to calculate the probabilities of a particle’s position, momentum, and other properties—evolves. Theoretical physicist Paul Dirac immediately realizes the enormous implications but also the challenges behind Schrödinger’s equation, which he summarized in his famous quote: “The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble.” From this point on, researchers concentrate on finding computationally affordable ways to exploit the predictive power of Schrödinger’s equation to design new chemicals and materials.
-
1927
Thomas-Fermi model
Physicists Enrico Fermi and Llewellyn Thomas use a statistical model they developed to approximate the distribution of electrons in an atom. The Thomas-Fermi model, a precursor to modern density functional theory, is the first attempt to develop a practical method to solve the many-electron Schrödinger equation in terms of electronic density instead of the full wave function.
-
Hartree method
Douglas Hartree, mathematician and physicist, introduces an approximate method to solve the Schrödinger equation, by writing the wave function as a product of single-particle functions called orbitals. The equations that need to be solved to obtain these orbitals must be solved iteratively: start from a guess for the solution, insert it into the equations, and get an updated solution, which goes back into the equations again. This procedure is repeated until input and output agree with each other. Later, the Hartree-Fock equations, Slater Xα method, and the Kohn-Sham equations of DFT will have to be solved with a similar iterative procedure, called self-consistent field.
-
1930
Hartree-Fock method
Physicist John Clarke Slater and Vladimir Fock independently realize that Hartree’s method does not satisfy the Pauli exclusion principle, which is key to describing the chemical diversity of atoms along the periodic table of elements. They therefore add an exchange term to Hartree’s equation. The resulting iterative Hartree-Fock equations are more complex to solve than Hartree’s much simpler ones, so researchers only start using this method when the first computers become available in the 1950s.
-
Thomas-Fermi-Dirac model
Similar to the work of Slater and Fock with the Hartree method, Paul Dirac adds a new term—the Dirac exchange—to the Thomas-Fermi model to approximate the effect of the Pauli principle in the model. Unfortunately, the Thomas-Fermi-Dirac model, which is much cheaper to solve than the Hartree-Fock equations, is still too inaccurate to be of practical relevance in chemistry.
-
1951
Slater Xα method
Since the Hartree-Fock equations are very demanding for computational resources at the time, Slater replaces the Hartree-Fock exchange operator with the Dirac exchange, which only depends on electron density. To make the method more accurate, Slater multiplies Dirac’s term by an adjustable parameter α, hence the name Xα. Quite surprisingly, Slater’s Xα method turns out be not only much cheaper than solving the full Hartree-Fock equations, but also more accurate in some cases. Slater’s Xα method can be seen as a first approximation to the Kohn-Sham equations with the local density approximation, which will appear only 15 years later.
-
1964
Hohenberg and Kohn theorems

Modern density functional theory begins with the publication of a landmark paper by Pierre Hohenberg, a theoretical physicist, and Walter Kohn, a mathematician and theoretical physicist, in Physical Review, a peer-reviewed scientific journal published by the American Physical Society. The theorems that Kohn and Hohenberg prove in their work lay the foundation for all modern density functional theories. The key result is the proof that a method based on electron density alone can be exact.
-
1965
Kohn-Sham equations
Working at the University of California, San Diego, Professor Walter Kohn and Lu Jeu Sham, who was then a postdoctoral fellow but later headed the UCSD Physics Department, introduce the Kohn-Sham equations. The Kohn-Sham equations are a crucial step in the evolution of density functional theory: the method becomes practically useful, as the Kohn-Sham model captures a large part of the DFT energy functional. At this point, there is only one term in Kohn-Sham DFT that remains unknown: the exchange-correlation functional. Although Kohn and Sham prove that the exchange-correlation functional is universal (the same for all molecules and materials), they are unable to write it down. All modern implementations of DFT use the Kohn-Sham equations, combined with an approximation for the exchange-correlation functional. The accuracy of Kohn-Sham DFT is determined by the quality of the exchange-correlation functional approximation.
-
Local-density approximation
Along with the Kohn-Sham equations, Walter Kohn and Lu Jeu Sham also introduced the first approximation for the exchange-correlation functional: the local density approximation (LDA). The LDA is the exact functional only if the density of the electrons is constant in space and does not vary. This situation does not correspond to any physical systems, but it is a very useful mathematical limit for the exchange-correlation functional. Kohn-Sham DFT with LDA proves reasonably accurate for describing simple metals and it becomes popular in solid-state physics. It is, however, not accurate enough for chemistry.
-
1980
Generalized gradient approximations
In the 1980s, theoretical physicists such as Axel Becke and John Perdew, and theoretical chemists such as Robert Parr, Weitao Yang, and others develop approximations for the exchange-correlation functional that use the gradient of the density, called generalized gradient approximations (GGAs). These are the first approximations that are accurate enough to become useful in chemistry. John Pople, who will share the 1998 Nobel Prize for Chemistry with Walter Kohn, is pivotal, together with Robert Parr and Evert Jan Baerends, in winning over the initial skepticism of chemists towards DFT. From here, DFT starts its rise to prominence, becoming more and more the workhorse method for computational chemistry.
-
1993
Hybrid functionals
Axel Becke proposes to mix some fraction of the Hartree-Fock exchange with some fraction of a GGA functional, creating what people would refer to as a hybrid functional. Hybrid functionals are more expensive than simpler GGAs, but can increase the accuracy for many chemical applications, although not always. Throughout the 1990s, the abundance of different approximations for the exchange-correlation functional starts to explode, as people propose various flavors of hybrid and GGA functionals. DFT is now the most widely used method in computational chemistry, providing an excellent compromise between cost and accuracy.
-
1998
Nobel Prize for DFT work

Walter Kohn receives a Nobel Prize in Chemistry for the Kohn–Sham equations, which he developed with fellow scientist Lu Jeu Sham in the mid-1960s, as well as his many other contributions to density functional theory over the past three decades.
-
2001
Jacob’s ladder of DFT
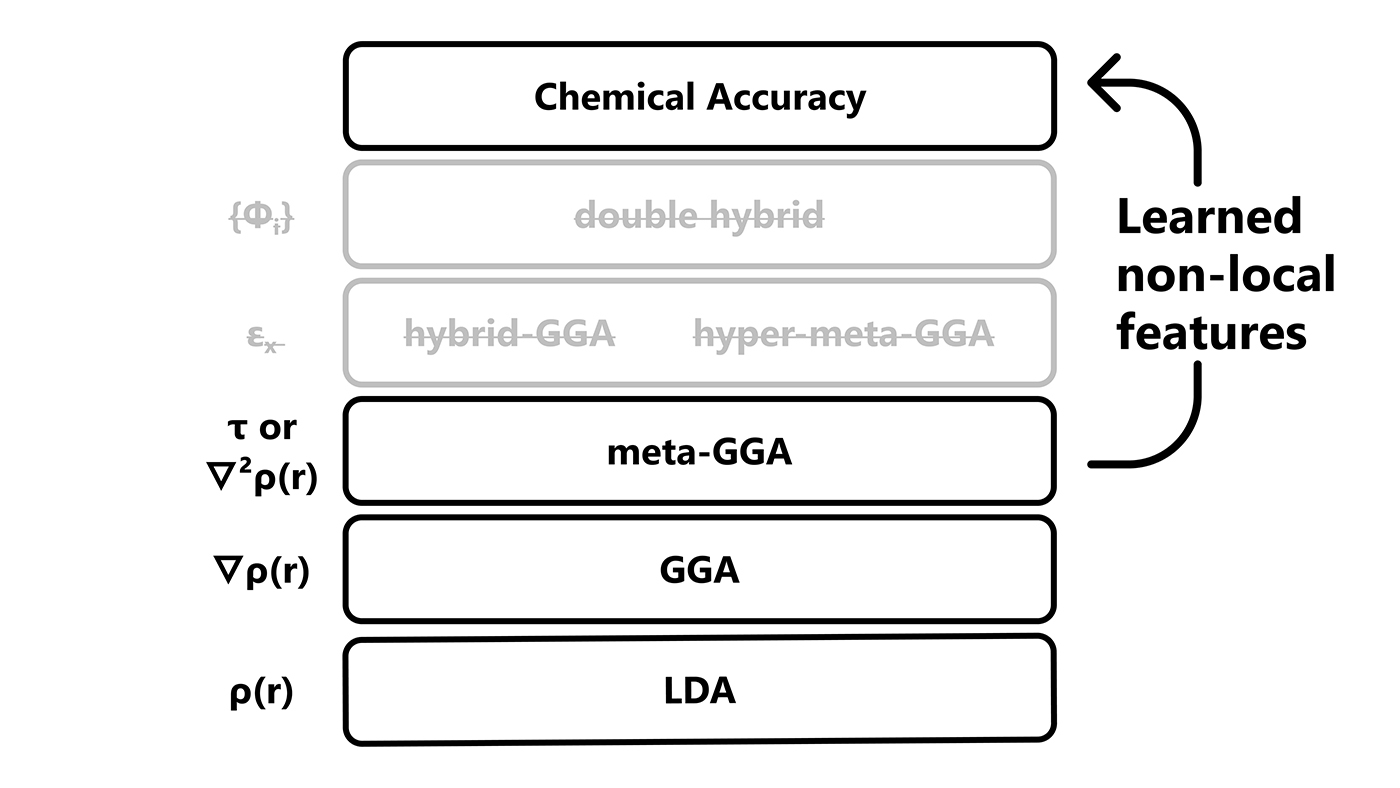
To classify the growing number of exchange-correlation approximations, John Perdew introduces the Jacob’s ladder of DFT. Like Jacob’s ladder in the Bible, the Jacob’s ladder of DFT is intended to bring users to the heaven of chemical accuracy, by adding more and more expensive ingredients to the functional. LDA is the lowest rung of the ladder, very cheap but not very accurate, with higher rungs corresponding to GGA and hybrid functionals. Going up the ladder, Perdew envisions using even more wave-function-like computationally costly ingredients to increase accuracy.
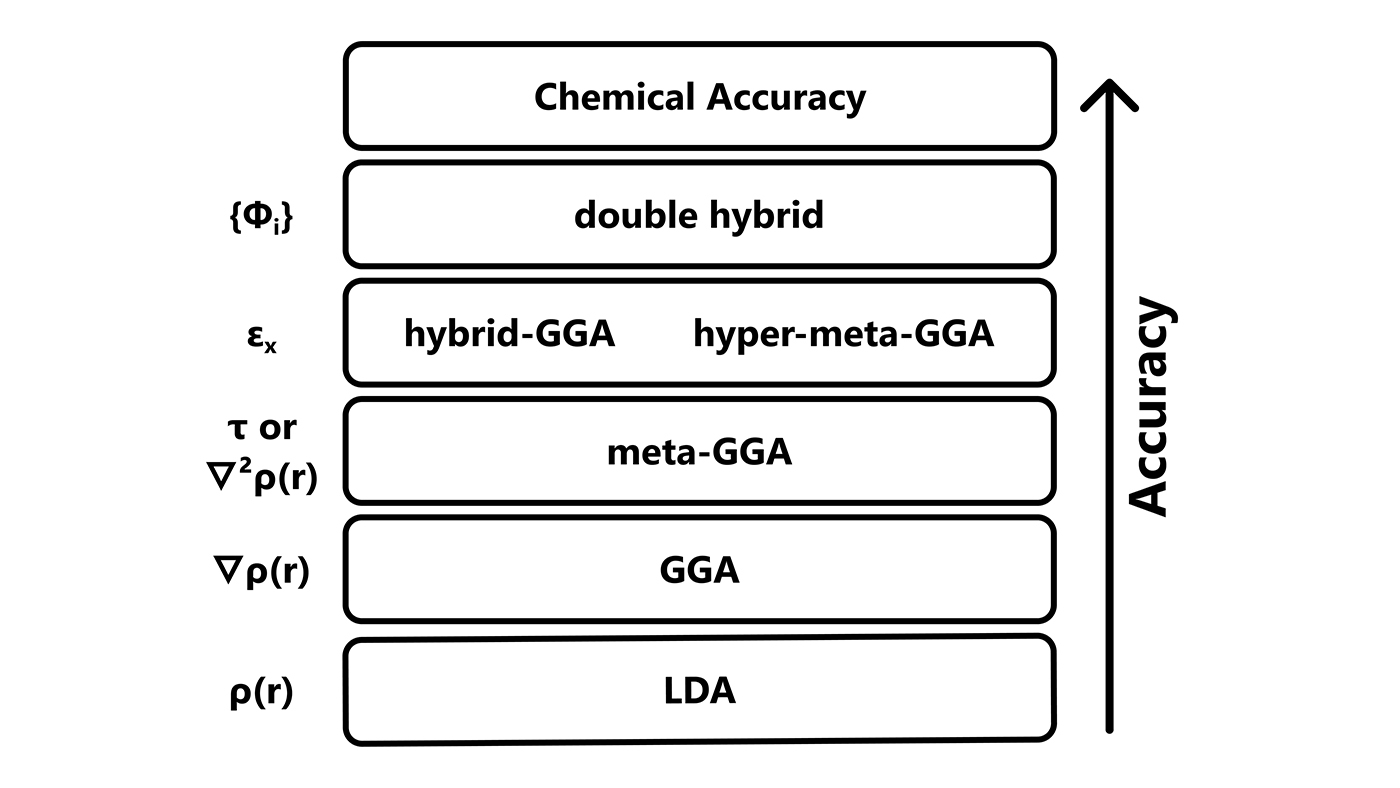
-
Trying to climb the ladder
From shortly after the turn of the century until today, the chase for more accurate exchange-correlation functionals continues, with people trying to climb the ladder by using some of the more expensive ingredients. It looks like there is an inescapable trade-off between accuracy and computational cost. Hundreds of approximations are now available to users, who must choose heuristically between them. Some of the most successful approximations are proposed by John Perdew, Axel Becke, Martin Head-Gordon, Donald Truhlar, Stefan Grimme, Gustavo Scuseria, Andreas Savin, Matthias Ernzerhof, and Jan Martin. The accuracy, however, is still not enough to really predict experiments. Even the few early machine learning attempts are based on the ingredients of Jacob’s ladder.
-
2025
Microsoft Research: Accuracy beyond the ladder
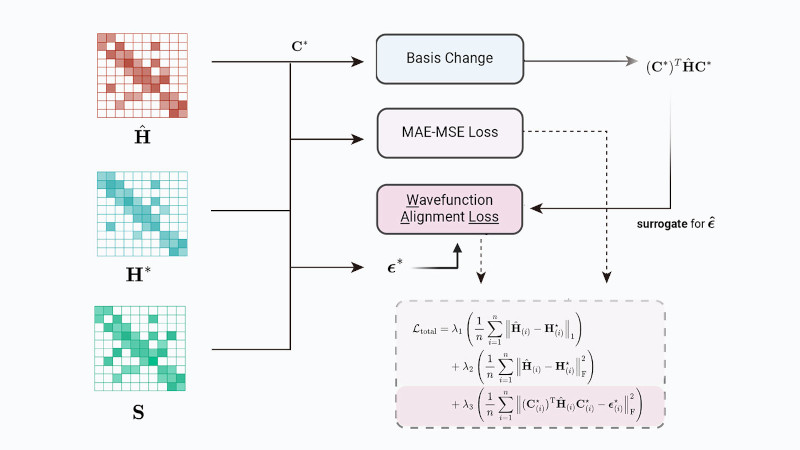
Microsoft researchers create a deep-learning-powered DFT model and train it on more than 100,000 data points, which is orders of magnitude beyond previous efforts and a major milestone in the field of quantum chemistry. By applying deep learning to DFT, Microsoft researchers let their model learn which features are relevant for accuracy, rather than relying on those from Jacob’s ladder, increasing accuracy without sacrificing efficiency, thus escaping the trade-off of accuracy and computational cost. This new way of building exchange-correlation models lays the foundation for a new era of density functional theory and other advancements in quantum chemistry as well as potential breakthroughs in drug discovery, materials science, and other fields.